微积分是什么?极限与微分初学者指南

微积分是一门研究函数变化率和无限小量积累的学科。微积分是什么?这篇文章为大家带来关于极限与微分初学者指南。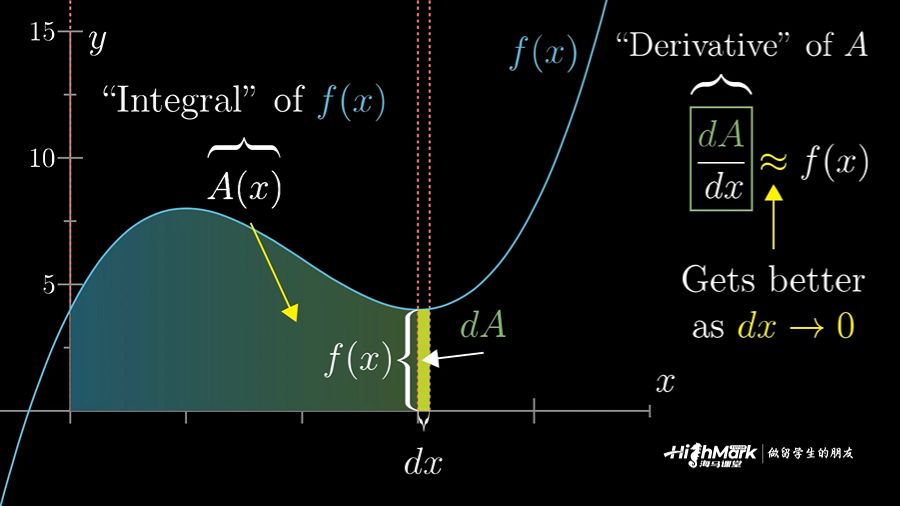

一、微积分分类

它大致可分为两个分支：

微分学。这涉及到量的变化率和在二维或多维空间中曲线或曲面的斜率。

积分学。这涉及到对无限小的量进行求和。

微积分是谁发明的?

微积分是由英国数学家、物理学家和天文学家艾萨克-牛顿和德国数学家戈特弗里德-威廉-莱布尼兹于 17 世纪分别独立发明的。

二、什么是微积分的应用?

微积分在数学、科学、工程学和经济学的各个领域广泛应用。

引言：函数的极限

要理解微积分，首先我们需要掌握函数的极限概念。

假设我们有一个连续线性函数，其方程如下所示：f(x) = x + 1，如下图所示。

f(x)的值简单地是x坐标的值加1。

f(x) = x + 1

该函数是连续的，这意味着f(x)对应于所有x的值，不仅仅是整数如-2、-1、0、1、2、3等等，还包括所有介于实数之间的值，即像7.23452这样的小数和像π和√3这样的无理数。

所以，如果x = 0，f(x) = 1

如果x = 2，f(x) = 3

如果x = 2.3，f(x) = 3.3

如果x = 3.1，f(x) = 4.1，依此类推。

让我们专注于x = 3，此时f(x) = 4。

当x越来越接近3时，f(x)也越来越接近4。

因此，我们可以令x = 2.999999，那么f(x)就是3.999999。

事实上，我们可以使f(x)越来越接近4。事实上，我们可以选择f(x)和4之间的任意小差距，相应地x和3之间的差距也会越来越小，但总会有一个更小的距离，使x和3之间的值更接近4。

那么函数的极限是什么呢?

再次参考图表，函数f(x)在x = 3处的极限是当x越来越接近3时，f(x)逐渐接近的值。而不是x=3处的f(x)的值，而是它逐渐接近的值。正如我们将在后面看到的，函数f(x)的值可能在某个x的特定值处不存在，或者可能是未定义的。

这可以表示为：“当x趋近于c时，f(x)的极限等于L”。

极限的正式定义

(ε，δ)柯西极限的定义

极限的正式定义由数学家奥古斯丁·路易·柯西和卡尔·韦尔斯特拉斯规定：

让f(x)是定义在实数R的一个子集D上的函数。

c是集合D中的一个点。 (在x = c处的f(x)的值可能不一定存在)

L是一个实数。

然后：

lim f(x) = L

x → c

存在，如果：

首先，对于每一个任意小的距离ε > 0，存在一个值δ，使得对于所有属于D的x和0 > | x - c | < δ，那么 | f(x) - L | < ε

其次，从兴趣x坐标的左侧和右侧逐渐接近的极限必须相等。

简单来说，这意味着当x趋近于c时，f(x)的极限是L，如果对于每个大于0的ε，存在一个值δ，使得c ± δ范围内的x值(不包括c本身，c + δ和c - δ)产生f(x)值在L ± ε范围内。换句话说，我们可以通过使x足够接近c来使f(x)尽可能接近L。

这个定义被称为删除极限，因为这个极限省略了点x = c。

极限的直观概念

通过使x足够接近c，但不等于c，我们可以使f(x)尽可能接近L。

函数的极限.0 > |x - c| 然后 0 > | f(x) - L | < ϵ

函数的极限.0 > |x - c| 然后 0 > | f(x) - L | < ϵ

连续和不连续函数

如果在实数线上某点x = c处定义了函数并且极限等于x = c处f(x)的值，则该函数在点x = c处是连续的，即：

lim f(x) = L = f(c)

x → c

连续函数f(x)是指在指定区间的每个点都是连续的函数。

连续函数的示例：

- 房间内的温度与时间。

- 随时间变化的汽车速度。

海马课堂专业课程辅导做出以下新改变啦：
⏩试听课全面升级，不满意退50%，
⏩课程辅导产品升级，赠送考前保障呦
⏩辅导不满意可以随心退！
海马课堂，3500+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、 难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。