悉尼大学双重积分哪家能辅导?

双重积分主要用于找到二维图形的表面积，通常用符号 '∫∫' 表示。我们可以通过双重积分轻松地找到矩形区域的面积。如果我们了解简单积分，那么解决双重积分问题将变得容易。因此，首先，我们将讨论一些积分的基本规则。

积分是微积分的重要部分，有许多类型的积分，如简单积分、双重积分和三重积分。通常，我们使用积分微积分来在很大的尺度上找到面积和体积，通过这种方式可以确定简单的公式或计算。

一、双重积分定义

在数学中，双重积分被定义为对两个变量的函数在二维平面上的某个区域的积分，即实数平面上的积分。两个变量的函数，比如 f(x, y)，在一个矩形区域上的双重积分可以表示为：

二、双重积分规则

在微积分中，我们通常遵循规则和公式来执行任何积分方法。要解决积分问题，您必须学习各种方法，如分部积分、替换积分或公式。在双重积分的情况下，我们将在这里讨论分部积分的双重积分规则，如下所示：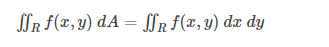

性质双重积分的性质如下：

∫x=ab ∫y=cd f(x,y)dy.dx = ∫y=cd∫x=ab f(x,y)dx.dy

∫∫(f(x,y) ± g(x,y)) dA = ∫∫f(x,y)dA ± ∫∫g(x,y)dA

如果 f(x,y) < g(x,y)，那么 ∫∫f(x,y)dA < ∫∫g(x,y)dA

k ∫∫f(x,y).dA = ∫∫k.f(x,y).dA

∫∫R∪Sf(x,y).dA = ∫∫Rf(x,y).dA+∫∫Sf(x,y).dA

三、双重积分面积

假设 z = f(x, y) 在xy平面上的一个区域D上定义，我们需要找到z的双重积分。如果我们将所需的区域分成垂直条纹，并仔细找到x和y的端点，也就是区域的限制，那么我们可以使用双重积分公式：

如果我们将所需的区域分成水平条纹，并仔细找到x和y的端点，也就是区域的限制，那么我们可以使用以下公式：

如果函数z是连续函数，那么：

四、极坐标中的双重积分

矩形坐标系中的双重积分可以转化为极坐标系中的双重积分，如下所示：

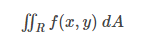
这也可以写成：

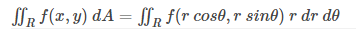
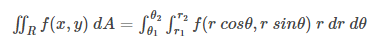
其中，

f(r cosθ, r sinθ) = f(r, θ)

在这种类型的双重积分中，首先我们要将f(r,θ)关于r在r = r1到r = r2的限制下积分，将θ视为常数，然后将得到的表达式关于θ从θ1到θ2积分。这里r1和r2可以是θ的常数或函数。

在这种情况下，首先我们要将f(r,θ)关于θ在θ = θ1到θ = θ2的限制下积分，将r视为常数，然后将得到的表达式关于r积分，这时θ的函数将是常数。

海马课堂专业课程辅导做出以下新改变啦：
⏩试听课全面升级，不满意退50%，
⏩课程辅导产品升级，赠送考前保障呦
⏩辅导不满意可以随心退！
海马课堂，3500+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、 难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。