澳洲国立大学实变函数课程太难怎么办?

人们通常只说实函数，这时人们会理解我们指的是实变量的实函数。其他类型的实函数(比如复变量的实函数)总是会被完整地明确指定。

对于数学家来说，这种对实函数的定义是完全令人满意的，因为所有已知映射的性质都可以轻松地转化为函数的性质。然而，对于数学的实际使用者来说，这可能不太合适，因为人们甚至可以在不知道一般映射的存在的情况下愉快高效地使用实函数，并且还可以使用较少的精确度。因此，我们将尝试在不涉及映射的情况下解释什么是实函数。

一、基本概念

实函数是一种指定参数值的规定。符号 y = f(x) 表示对于参数值 x，函数 f 分配了值 y。有时我们还使用符号 f : x ↦ y，换句话说，函数 f 将 x 映射到 y。最常用的指定这种分配方式的方法是通过某个公式，也就是说，函数值 y 可以通过将 x 替换为一个特定的公式来获得，该公式标识了给定的函数。例如，函数 f(x) = 2x + 3 将参数 x = -1 映射为 f(-1) = 2*(-1) + 3 = 1。一个非常特殊的情况是常数函数，例如定义 g(x) = 7.3 将每个参数 x 映射到值 7.3;这对于初学者而言有时可能会让人困惑，所以请将其视为一个警告，即可以将 x "代入" 7.3，结果就是 7.3(就像这样：g(5) = 7.3)。

还有一种表达将某个具体数字代入函数的方法。它使用了稍微降低的竖线，过程如下：

这种符号在函数还没有准备好进行代入操作，但我们想要进行一些调整时特别方便。例如，

最好的可视化函数的方法是通过图形，我们在二维平面(x，y)上标记所有的对偶(x，f(x))。我们在图片中指出了一个特定的对偶。

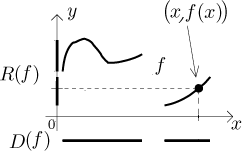
请注意，如果函数由一个公式给出，我们可能还对其代数结构感兴趣，这是另一种从独立于图形观点的方式来看待它。详细信息请参阅关于求值顺序的说明。

函数的定义域有时在函数定义时给出。更常见的情况是，实函数只是以规定、公式的形式给出，在这种情况下，我们将定义域视为所有可以代入函数的数字 x 的集合，也就是说，对于那些使得定义函数的公式有意义的 x 值。通常用 D( f )、Df 或 dom( f ) 表示，这里我们将使用第一种符号。我们可以写成

D( f ) = {x∈ℝ;  f (x) makes sense}.

通常，定义域将是一些区间的并集。

函数的值域是通过将来自定义域的参数代入函数获得的所有值的集合。通常用 R( f )、Rf 或 ran( f ) 表示，这里我们将使用第一种符号。我们可以写成

R( f ) = { f (x); x∈D( f )}.

有时只考虑给定函数在定义域的子集上的情况。这时我们称函数被限制在了这个子集上，新函数被称为限制。如果 M 是函数 f 的定义域 D( f ) 的子集，那么 f 在集合 M 上的限制记作 f |M。

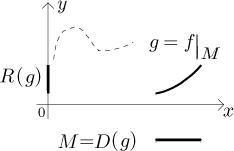
被限制的函数具有不同的定义域，也可能有不同的值域(虽然这并非必然，有时函数可以在我们限制的子集上覆盖其所有值，并且只在被忽略的部分重复这些值)。

函数的性质在很大程度上取决于它们的定义域，因此实际上我们必须始终将函数和它们的定义域视为一对。

海马课堂专业课程辅导，2100+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、 难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。