诺丁汉特伦特大学解析几何课程辅导

点击蓝字可以直接获取专业的解析几何课程辅导！

一、什么是解析几何?

解析几何是数学的一个重要分支，它有助于在二维平面中表示几何图形并了解这些图形的性质。在这里，我们将尝试了解坐标平面和一个点的坐标，以初步了解解析几何。

1.坐标平面

笛卡尔平面将平面空间分为二维，对于轻松定位点很有用。它也被称为坐标平面。坐标平面的两个轴是水平的 x 轴和垂直的 y 轴。这些坐标轴将平面分为四个象限，这些轴的交点是原点 (0. 0)。此外，坐标平面中的任何一点都用点 (x, y) 表示，其中 x 值是该点相对于 x 轴的位置，y 值是该点相对于 y 轴的位置。

坐标平面四个象限中表示的点的性质如下：

原点 O 是 x 轴和 y 轴的交点，坐标为 (0. 0)。

原点 O 右侧的 x 轴是正 x 轴，原点 O 左侧的是负 x 轴。同样，原点 O 上方的 y 轴是正 y 轴，原点 O 下方的是负 y 轴。

在第一象限中表示的点 (x, y) 具有两个正值，并参照正 x 轴和正 y 轴绘制。

在第二象限中表示的点是 (-x, y)，参照负 x 轴和正 y 轴绘制。

在第三象限中表示的点 (-x, -y) 参照负 x 轴和负 y 轴绘制。

在第四象限中表示的点 (x, -y) 参照正 x 轴和负 y 轴绘制。

解析几何 —— 坐标平面

2.一个点的坐标

坐标是一个地址，有助于在空间中定位一个点。对于二维空间，一个点的坐标是 (x, y)。在这里，让我们注意这两个重要的术语。

横坐标：它是点 (x, y) 中的 x 值，它是该点沿 x 轴距原点的距离。

纵坐标：它是点 (x, y) 中的 y 值，它是该点垂直于 x 轴的距离，平行于 y 轴。

一个点的坐标对于执行许多操作很有用，例如求距离、中点、直线的斜率、直线方程。

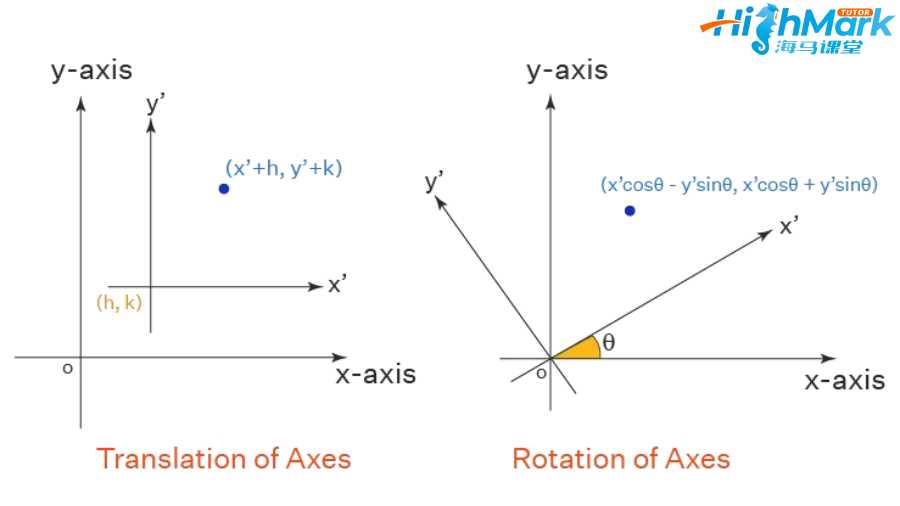
解析几何 —— 坐标轴的平移和旋转

解析几何中的坐标轴可以通过移动坐标轴进行平移，使得新坐标轴与旧坐标轴平行。坐标轴也可以绕原点相对于 x 轴旋转一定角度。让我们在下面的句子中进一步了解坐标轴的平移和旋转。

4.坐标轴的平移

以原点为 O 的给定坐标轴上一点的坐标为 (x, y)。在这里，我们将原点转移到一个新原点 O'，新原点 O' 相对于旧坐标轴位于点 (h, k) 处。新坐标轴进行平移，使得新坐标轴与旧坐标轴平行。一个点的坐标从 (x, y) 转换为 (x' + h, y' + k)。任何关于旧坐标轴的直线或曲线方程，都可以通过简单地将方程中的 (x, y) 替换为 (x + h, y + k) 轻松转换为关于新坐标轴的方程。

5.坐标轴的旋转

坐标轴 ox 和 oy 逆时针旋转一个角度 θ，得到新坐标轴 ox' 和 oy'。一个点相对于旧坐标轴的坐标是 (x, y)，旋转后，相对于新坐标轴的坐标是 (x', y')。此外，我们可以通过将 (x', y') 替换为 (xCosθ - ySinθ, xSinθ + yCosθ) 来恢复旧坐标。

海马课堂，4000+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、 难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。