华盛顿大学AMATH 351 A: 微分方程及应用导论

微积分是研究变化的数学，而变化的速率通常由导数表示。因此，使用微积分的最常见方式之一是建立一个包含未知函数 y=f(x) 及其导数(称为微分方程)的方程。解决这种方程通常提供关于数量如何变化以及变化发生的原因的信息。这篇文章为大家带来关于华盛顿大学AMATH 351 A: 微分方程及应用导论的讲解。

一、课程描述

本课程是继学习微积分(MATH 124 和 125)之后的第一门微分方程课程。在本课程中，我们将通过物理、化学、生物科学和工程学中的实例来学习如何求解常微分方程(ODE)。我们的大部分理论讨论都来自应用。

现在有一些软件可以为我们得到 ODE 的解析解。因此，对我们来说，更重要的是理解隐藏在不同求解方法背后的逻辑，而不仅仅是熟悉如何摇动求解机器。这样，我们就能理解一种求解方法为何有效，并有可能在未来开发出求解 ODE 的新方法。

二、先决条件

熟练掌握代数方程的运算、极限的评估、微分和积分的方法，达到 MATH 124 和 125 的水平。我们将介绍和使用与我们相关的线性代数、少量复变函数和幂级数。如果您以前接触过线性代数、复变函数和泰勒级数，将会有所帮助。

三、一般微分方程

考虑方程 y'=3x^2，这是微分方程的一个示例，因为它包括一个导数。变量 x 和 y 之间存在关系：y 是 x 的一个未知函数。此外，方程的左侧是 y 的导数。因此，我们可以这样解释这个方程：从某个函数 y=f(x) 开始，然后对它进行求导。答案必须等于3x^2。哪个函数的导数等于3x^2?其中一个这样的函数是 y=x^3，因此这个函数被认为是微分方程的一个解。

定义：微分方程

微分方程是一个涉及未知函数 y=f(x) 及其一个或多个导数的方程。微分方程的解是一个函数 y=f(x)，当将 f 及其导数代入方程时满足微分方程的函数。

四、一般解和特解

我们已经注意到微分方程 y'=2x 至少有两个解：y=x^2 和y=x^2+4。这两个解之间唯一的区别是最后一项，即一个常数。如果最后一项是一个不同的常数会怎样呢?这个表达式仍然会是微分方程的解吗?事实上，任何形式为y=x^2+C的函数，其中C代表任意常数，也是一个解。原因是x^2+C的导数是2x，不管C的值如何。可以证明，这个微分方程的任何解都必须具有y=x^2+C的形式。这是微分方程的一般解的示例。一些这些解的图形如图所示。(注意：在这个图中，我们使用了范围在-4到4之间的偶数值C。实际上，C的值没有限制;它可以是整数或其他值。)

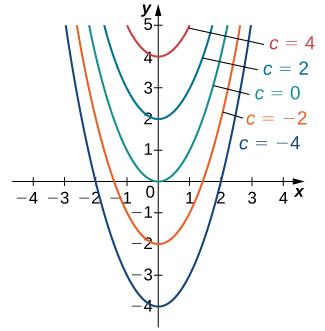
在这个示例中，我们可以自由选择任何我们希望的解；例如，y=x^2−3是这个微分方程解的一部分。这被称为微分方程的特解。如果我们获得有关问题的额外信息，通常可以唯一确定特定的解。

海马课堂专业课程辅导做出以下新改变啦：
⏩试听课全面升级，不满意退50%，
⏩课程辅导产品升级，赠送考前保障呦
⏩辅导不满意可以随心退！
海马课堂，3500+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、 难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。