首页 > 留学资讯 > 美国留学辅导 > 埃塞克斯大学伽罗瓦理论辅导

埃塞克斯大学伽罗瓦理论辅导

作者：海马发布时间：2023-10-23 12:32:02

也许你听说过Évariste Galois吗?(发音为“GAL-wah”)。今天我们将俯瞰他在数学领域最著名的贡献：恰如其名的Galois理论。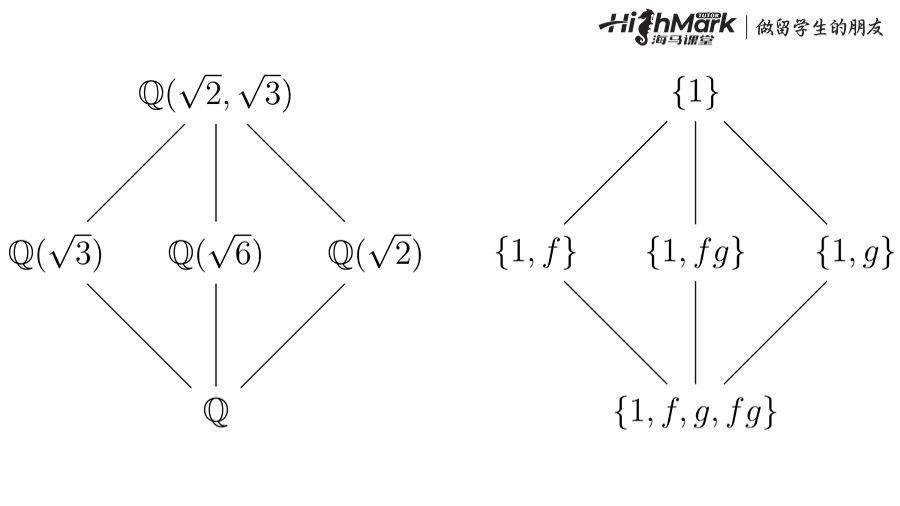 Galois theory

一、

如果你是即将学习Galois理论的学生，希望下面的信息能为你的主课程提供一点前菜。在下面的“从英语到数学”部分，我们将简要介绍标准研究生课程中出现的思想，这样当你开始做练习时，至少能有一个鸟瞰全貌的了解。

二、

即使你不打算学习Galois理论，只是出于好奇，这篇文章也适合你!这里的信息应该对具有至少本科抽象代数背景的任何人都是可访问的。我将略去很多技术细节(但你不介意，对吧?)因为我在这里的目标只是传达一些主要思想。希望这能激起你进一步学习的兴趣。

总之，Galois理论揭示了群的结构与域的结构之间的关系。然后利用这种关系来描述多项式的根是如何相互关联的。

更具体地说，我们从一个多项式 f(x)开始。它的根存在于一个域中(称为 f(x)的分裂域)。这些根展示出一种对称性，通过让某个特定的群(称为 f(x)的Galois群)对它们进行操作来看到。我们可以通过Galois基本定理从域的结构和反之亦然收集关于群的结构的信息：

现在，为什么有人会关心排列多项式的根呢?这有什么好处?嗯，二次方程的公式在Galois出现之前就是众所周知的(实际上可以追溯到巴比伦人)。因此，自然地，数学家们想知道，“是否存在类似的公式，适用于更高次的多项式?”换句话说，是否可以将n次多项式的根写成多项式系数的某种代数组合(加、减、乘、除、开方)?事实证明，当n≤4时，答案是“是”，但对于任何n≥5，答案是“否”。

正是Galois对多项式根的排列群的研究导致了他发现寻找这种公式的必要和充分条件的发现。这个条件(数学家们寻找了300多年!)在将问题从域论的语言转化为群论的语言时变得非常明确。Galois理论就是实现这一点的字典。

海马课堂专业课程辅导做出以下新改变啦：
⏩试听课全面升级，不满意退50%，
⏩课程辅导产品升级，赠送考前保障呦
⏩辅导不满意可以随心退！
海马课堂，3500+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。