首页 > 留学资讯 > 美国留学辅导 > HighMark复变函数学习难点解析

HighMark复变函数学习难点解析

在传统数学中，复数分析被称为复变函数理论。它是数学分析中分析复数函数的分支。它对数学的多个分支都有帮助，包括数论、代数几何、解析组合学和应用数学。在本文中，您将了解什么是复变函数，以及如何求解复变函数。这篇文章HighMark为大家带来复变函数学习难点解析。

一、复变函数的定义

复变函数或复变函数是为复数赋复数的函数。假设 C 是复数集合。

函数 f : C → C 是一个规则，它与 z∈ C 相关联，是唯一的 w∈ C，写成 w = f(z)。在这里，

z = x + iy

w = u + iv, where u = u(x, y) and v = v(x, y)

因此，u 和 v 是 x 和 y 的函数。

w = f(z) = u(x, y) + i v(x, y)

此外，w 的实部和虚部的标准符号是 u 和 v，其中 u 和 v 是 x 和 y 的函数。请注意，这里，D 称为函数 f 的定义域。复变函数，即 w = f(z)，通常表示为从复平面 z 到复平面 w 的映射或变换：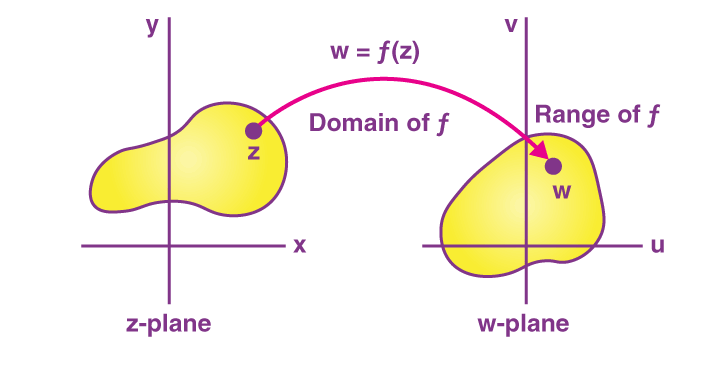

函数的图形通常揭示了实变实值函数的性质。然而，对于函数 w = f(z)，其中 z 和 w 都是复数，却没有合适的图形表示法，因为数字 z 和 w 位于平面而非直线上。

二、已解决实例讲解

示例：

考虑 f(z) = z2 + iz，并用实部和虚部表示。

解决方案：

我们知道，z = x + iy

现在，f(z) = z2 + iz

= (x + iy)2 + i(x + iy)

= x2 + i2y2 + 2ixy + ix + i2y

= x2 – y2 + 2ixy + ix – y {since i2 = -1}

= x2 – y2 – y + i(x + 2xy)

其形式为w = u + iv such that u = x2 – y2 – y and v = x + 2xy.

或者

u = u(x, y) = x2 – y2 – y

v = v(x, y) = x + 2xy

海马课堂专业课程辅导，2100+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。