首页 > 留学资讯 > 美国留学辅导 > Gamma Distribution主要讲什么内容?美国留学生不懂怎么办?

Gamma Distribution主要讲什么内容?美国留学生不懂怎么办?

作者：海马发布时间：2023-11-24 10:53:42

伽马分布(Gamma Distribution)是广泛应用于商业、科学和工程领域的分布之一，用于对具有正偏态分布的连续变量进行建模。伽马分布是一种与贝塔分布相关的统计分布。在泊松分布事件之间的等待时间彼此相关的情况下，这种分布自然产生。本文将结合实例讨论伽马分布所涉及的参数、公式、图形、性质、均值、方差。

Gamma Distribution主要讲什么内容?美国留学生在学习这部分知识学不懂怎么办?HighMark课程辅导会给大家带来专业的辅导!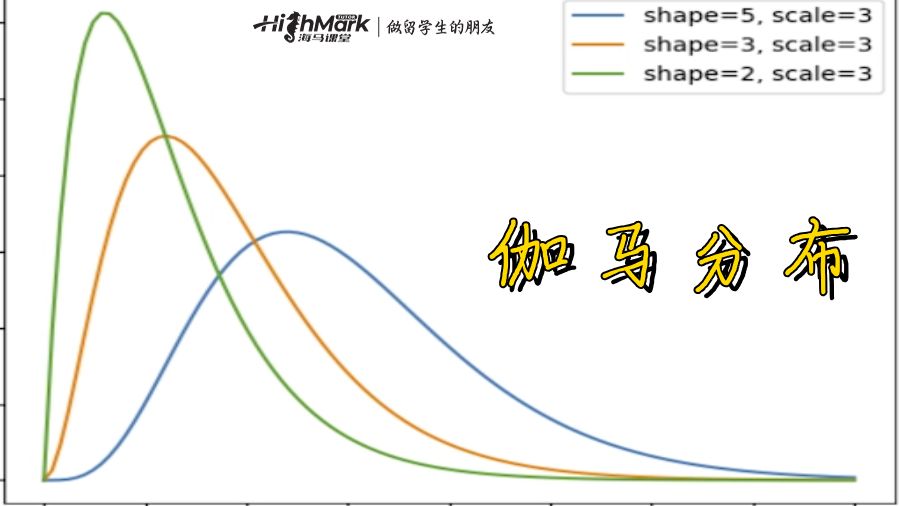 伽马分布(Gamma Distribution)

一、什么是伽玛分布

伽玛分布是一个概率分布术语，通常用来描述具有连续概率分布的分布，其定义由两个参数确定，即形状参数和逆尺度参数。伽玛分布与正态分布、指数分布、卡方分布和埃尔朗分布有关。符号‘Γ’代表伽玛函数。

伽玛分布有两个自由参数，分别称为α(形状参数)和β(速率参数，即尺度参数的倒数)，其中：

α = 形状参数

β = 速率参数(尺度参数的倒数)

其特征是均值 µ=αβ 和方差 σ²=αβ²。

尺度参数β仅用于调整分布。可以通过观察，在概率密度中无论随机变量x出现在何处，都会除以β。由于尺度参数提供了尺度数据，因此很少有必要使用“标准”伽玛分布，即β=1。

二、伽玛分布函数

伽玛函数由Γ(y)表示，它是阶乘函数对复数(实数)的扩展形式。因此，如果n∈{1,2,3,…}，那么Γ(y)=(n-1)!

三、伽玛分布图

伽玛分布的参数定义了图形的形状。形状参数α和速率参数β都大于1。

当α = 1时，它变为指数分布。

当β = 1时，它变为标准伽玛分布。

海马课堂专业课程辅导做出以下新改变啦：
⏩试听课全面升级，不满意退50%，
⏩课程辅导产品升级，赠送考前保障呦
⏩辅导不满意可以随心退！
海马课堂，3500+严选硕博学霸师资，针对学生的薄弱科目和学校教学进度，匹配背景相符的导师，根据学生情况进行1V1专属备课，上课时间灵活安排，中英双语详细讲解课程中的考点、难点问题，并提供多方位的课后辅导，辅助学生掌握全部课程知识，补足短板。